位运算

摘要：本篇文章主要讲解位运算

一、位运算

前言：

程序中得所有数都以二进制形式存在计算机内存中，位运算就是直接对2进制本身进行操作。

所有数之间的位运算都应当转换为二进制再进行计算

1. and：&

• 计算规则：全1得1，其余得0

• 常见用处：通常用于二进制取位操作，构造一个与目标同位数的数，并把想要取位的位置设为1即可。

• 例子

  1、num & 1 判奇偶，结果是1为奇数，结果是0为偶数

2. or ：|

• 计算规则：有1得1，全0为0

• 常见用处：通常用于二进制特定位上的无条件赋值

• 例子：

  1、一个数or 1的结果就是把最末位强行变成1。

  2、想要把最末位变成0，可以通过or 1 后再减 1 即可

  实际意义：求这个数最近的奇数或偶数

3. xor：^（其实就是大名鼎鼎的异或）

• 计算规则（二进制）：数学定义
  $$
  a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
  $$
  理解起来就是：相同为0，不同为1

  异或的第二种理解：取反

  即0异或别人，相当于没异或。1异或别人，异或了，取反了，1变0，0变1。

• 常见用处：对二进制特定位置取反，只要把运算数那个位置设为1就好了

• 异或的逆运算是本身。逆运算：一个数经过另一个数的运算和逆运算后应该不变，对于异或而言就是它本身

异或运算的十进制角度

1. 交换律：a ^ b ^ c <=> a ^ c ^ b
2. 任何数于0异或为任何数 0 ^ n => n
3. 相同的数异或为0: n ^ n => 0

交换律：从数学定义上看，ab换位置无所谓，从二进制原理角度看，谁前谁后也无所谓

4. not运算

• 计算规则：将全部二进制位取反
• 如果not的对象是无符号整数（不能表示负数），那么得到的值就是它与该类型上界的差

5. 左移运算（<<）

• 计算规则：把a转为二进制后左移b位（在后面添b个0）

  关于二进制：二进制从$2^0$开始，前四位代表$2^0-2^3$。

  例如：

  （100<<2）100的二进制为1100100，左移两位后110010000为400，即（100<<2）= 100 * $2^2$ = 400

  a shl b的值实际上就是a乘以2的b次方，因为在二进制数后添一个0就相当于该数乘以2。

• 通常认为a shl 1比a * 2更快，因为前者是更底层一些的操作。因此程序中乘以2的操作请尽量用左移一位来代替

6. 右移运算（>>）

• 计算规则：a shr b表示二进制右移b位（去掉末b位），相当于a除以2的b次方（取整）
• 用shr代替除法运算可以使程序效率大大提高。最大公约数的二进制算法用除以2操作来代替慢得出奇的mod运算，效率可以提高60%。

常见操作

补：

1. 判断数偶： 奇数 x&1 == 1 偶数 x&1 == 0
2. 两数取平均(除2): mid = (left+right)/2 等价于 mid = (left+right) >> 1
3. 清除最低位的1: x = x&(x-1)
4. 得到最低位的1: n = x & -x
5. 清零: x&~x

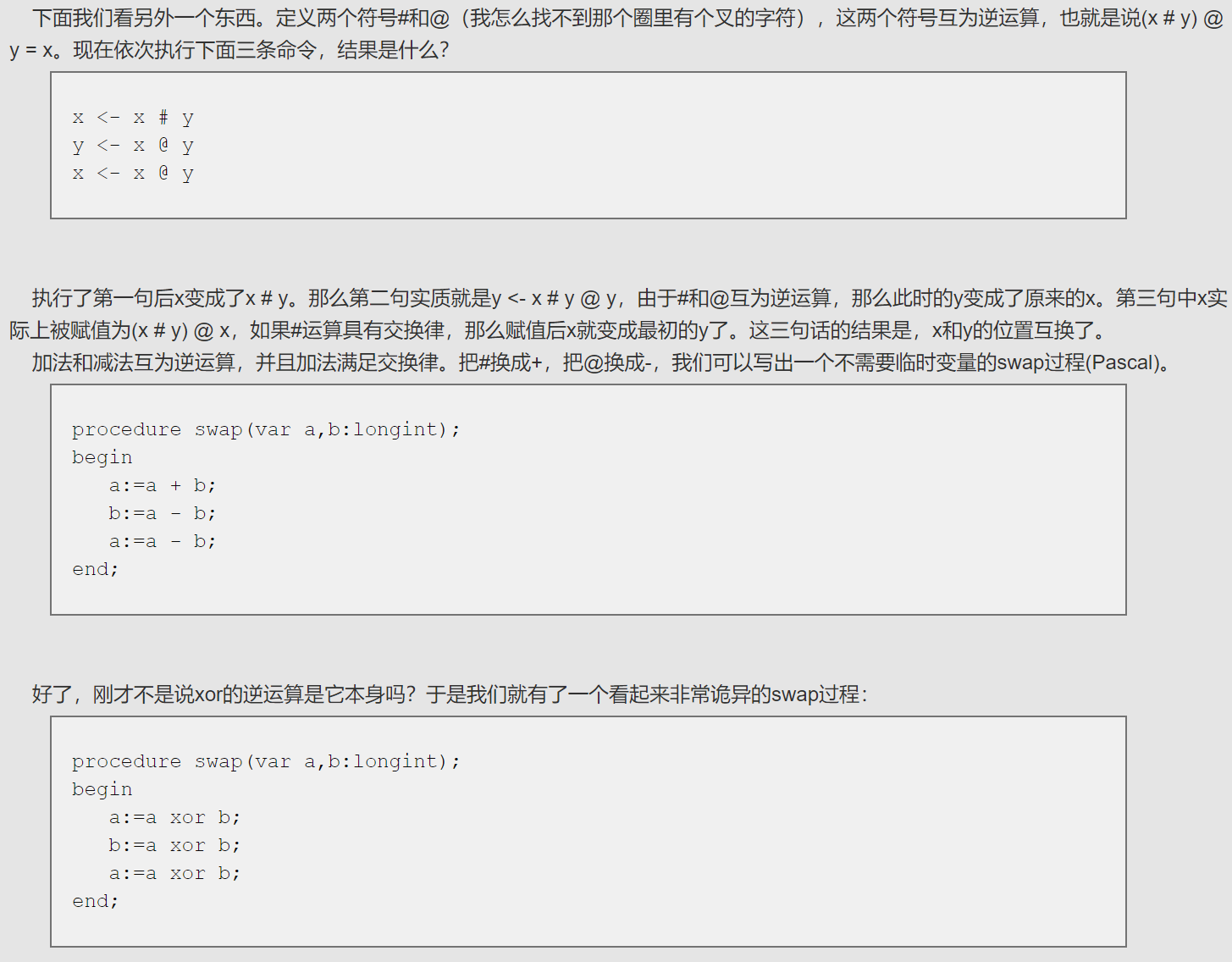
不使用额外空间的交换——不需要额外空间的方法，就往位运算上想

补充：

计算1的个数：动态规划移位

赏

谢谢你请我吃糖果